В этой статье, состоящей из двух частей, мы рассмотрим некоторые из сложнейших математических задач, которые остаются нерешенными по сей день.

На решение многих математических задач у математиков уходят десятилетия и даже столетия, в то время как другие задачи даже не поддаются решению. Любой, кто сможет решить некоторые из нерешенных задач, получит значительное финансовое вознаграждение, что поощрит математиков принять такой вызов.
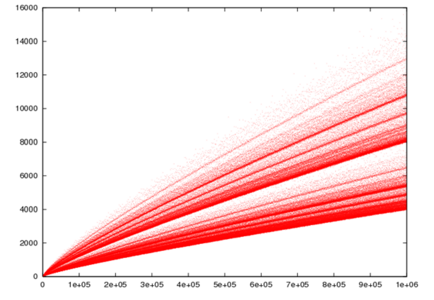
Гипотеза Коллатца включает в себя генерацию последовательностей целых чисел, где каждое число получается из предыдущего по двум правилам. Начиная с любого положительного целого числа, если число четное, то его следует разделить на 2, а если нечетное — умножить на 3 и добавить 1, и в конечном итоге последовательность всегда достигнет числа 1.
Например, если мы начнем с числа 5, следующим числом будет 3x5+1, что равно 16. Поскольку 16 четное, мы разделим его на 2, чтобы получить следующее число в последовательности: 8. Это продолжается до тех пор, пока оно не достигнет 1. В итоге последовательность будет такой: 5, 16, 8, 4, 2, 1.
Главный вопрос гипотезы – всегда ли эта последовательность достигнет 1, независимо от начального положительного целого числа? Гипотеза Коллатца была выдвинута немецким математиком Лотаром Коллатцем в 1937 году, всего через 2 года после того, как он получил докторскую степень.
На протяжении многих лет математики пытались разгадать тайну гипотезы Коллатца, но она так и осталась загадкой. Многие математики предполагают, что эта проблема может быть даже вне досягаемости современной математики. Несмотря на многочисленные усилия, вложенные в исследование гипотезы, она остается нерешенной, и математическое сообщество продолжает бороться с ее тонкостями
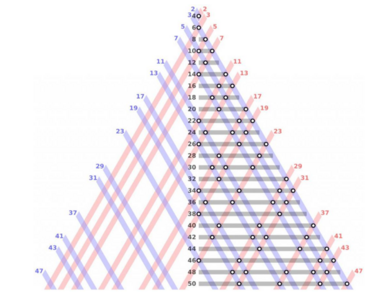
Гипотеза была впервые предложена Кристианом Гольдбахом в письме Леонарду Эйлеру от 7 июня 1742 года. В этом письме Гольдбах представил идею и предположил, что каждое целое число, большее 2, можно выразить как сумму трех простых чисел.
Эйлер в своем ответе счел первую часть гипотезы Гольдбаха весьма вероятной, заявив, что «всякое четное целое число является суммой двух простых чисел», хотя и не смог предоставить доказательства.
За прошедшие годы был достигнут значительный прогресс в понимании этой гипотезы. Например, Нильс Пиппинг проверил это утверждение до n = 100 000 в 1938 году, а позже, с появлением компьютеров, Т. Оливейра и Сильва провел распределенный компьютерный поиск, который подтвердил гипотезу для n, меньшего или равного 4×1018. (и перепроверено до 4×1017) к 2013 году.
Однако полное и строгое доказательство для всех четных целых чисел больше 2 остается неуловимым.
Другими словами, если p является простым числом, то существует вероятность, что p+2 тоже будет простым числом, и эти два простых числа будут образовывать пару простых чисел-близнецов. Примеры пар простых чисел-близнецов: (3, 5), (11, 13), (17, 19), (29, 31) и так далее.
Доказательство гипотезы о простых числах-близнецах долгое время было открытым вопросом в теории чисел. Первоначально это было предложено Альфонсом де Полиньяком в 1849 году, предполагавшим, что для каждого натурального числа k существует бесконечно много простых чисел p, таких что p+2k также является простым. Случай k=1 — это конкретная гипотеза о простых числах-близнецах, на которой мы сосредоточены.
В 2013 году работа математика Итана Чжана ознаменовала значительный шаг на пути к доказательству существования бесконечного числа простых чисел-близнецов. Исследования Чжана показали, что существует конечная верхняя граница – 70 миллионов – для которой промежутки между парами простых чисел сохраняются бесконечно часто.
В 2014 году граница (разница между двумя простыми числами) сократилась до 246, что указывает на значительный прогресс в понимании простых чисел-близнецов.
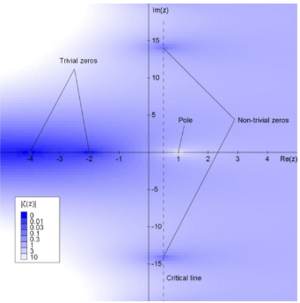
Гипотеза Римана касается поведения дзета-функции Римана — математической функции, используемой для изучения распределения простых чисел в комплексной плоскости. Риман утверждает, что все нетривиальные нули дзета-функции Римана лежат на определенной критической линии в комплексной плоскости. Мы можем думать об этой критической линии как о натянутом канате, и вопрос в том, изящно ли балансируют все эти нули на этой линии.
История гипотезы Римана начинается в XIX веке с немецкого математика Бернхарда Римана. В 1859 году Риман опубликовал основополагающую статью под названием «О количестве простых чисел, меньших заданной величины» (On the Number of Prime Numbers less than a Given Quantity). На страницах документа математик представил дзета-функцию ζ(s), комплексную функцию комплексной переменной 's'. Открытие Римана было революционным, поскольку оно потенциально могло раскрыть тайны простых чисел.
Гипотеза Римана имеет еще значительный вес в математическом мире благодаря ее включению в престижную «Задачу тысячелетия». В 2000 году Институт математики Клея признал гипотезу одной из семи выдающихся математических задач и предложил приз в 1 миллион долларов тому, кто сможет предоставить правильное доказательство одной из семи задач.
Сущность значения гипотезы Римана заключается в ее связи с теоремой о простых числах. В частности, если гипотеза Римана будет доказана или опровергнута, то многие важные теоремы о простых числах, опирающиеся в доказательстве на гипотезу Римана, станут либо истинными, либо ложными.
Или другой хорошо известный пример совершенного числа — 28, делители которого равны 1, 2, 4, 7 и 14, и в сумме (1 + 2 + 4 + 7 + 14) дают 28.
Однако остается неясным, существуют ли какие-либо нечетные совершенные числа.
Правило Евклида для нахождения совершенных чисел заключается в том, что если 2n – 1 является простым числом (такое число называется простым числом Мерсенна), то 2n-1 (2n – 1) будет совершенным числом. Все известные совершенные числа были найдены именно таким образом и все они четные.
Жак Лефевр в 1496 году предположил, что все совершенные числа могут быть найдены по правилу Евклида, что подразумевает, что нечетных совершенных чисел не существует. Леонард Эйлер в свою очередь заметил, что вопрос о существовании нечетных совершенных чисел является чрезвычайно трудным и до сих пор не решенным.
Карл Померанс в более позднее время представил эвристический аргумент, утверждающий, что вероятность существования нечетных совершенных чисел очень мала. Это не доказывает их отсутствие, но усиливает сомнения в их существовании. Таким образом, несмотря на многовековые исследования, вопрос о существовании нечетных совершенных чисел остается открытым и является одной из загадок в теории чисел.
Рассматриваемая проблема вращается вокруг трансцендентной природы некоторых математических констант, в частности константы Эйлера-Машерони (γ) и суммы π (pi) и e (числа Эйлера).
Трансцендентное число — это число, которое не является корнем какого-либо ненулевого полиномиального уравнения с целыми коэффициентами. Проще говоря, трансцендентные числа не могут быть выражены как решение полиномиального уравнения, в котором коэффициенты являются целыми числами.
Полиномиальное уравнение — это математическое уравнение, в котором полином равен нулю. Полином – математическое выражение, состоящее из переменных и коэффициентов, которые соединяются операциями сложения, вычитания, умножения и ненулевыми целочисленными степенями переменных. Например, x2+3x+2 является полиномом
Константа Эйлера-Машерони, обозначаемая как γ, является фундаментальной математической константой, которая возникает в различных областях математики, включая теорию чисел и исчисление.
Трансцендентный статус был предметом предположений в течение многих лет. Хотя существуют существенные доказательства, указывающие на трансцендентную природу γ, строгое доказательство остается нераскрытым.
Аналогично, сумма π и e является еще одним примером. И π, и e — трансцендентные числа, и ожидается, что их сумма также будет трансцендентной. Однако эта гипотеза еще не была окончательно доказана, что добавляет элемент загадочности в математический мир.
Статус этих констант как трансцендентных или нет, выходит за рамки математического любопытства и имеет значение в различных математических дисциплинах.
К одиночным числам относятся простые числа, степени простых чисел и те числа, у которых наибольший общий делитель числа и сумма его делителей (обозначаемая как сигма (n)) равны 1. Например, цифра 5 — это одиночное число. Делителями 5 являются 1 и 5, а их сумма равна 6. Наибольший общий делитель 5 и 6 равен 1.
Хотя одиночество некоторых чисел можно доказать, исследуя их свойства, есть другие, для которых доказательство одиночества является сложной задачей. Например, считается, что такие числа, как 10, 15, 20 и многие другие, являются одиночными, но убедительного доказательства не существует.
Концепция одиночных чисел уже много лет интригует математиков. Хотя простые числа являются хорошо известными одиночными числами, другие целые числа также демонстрируют одиночество, даже если они не имеют общего наибольшего общего делителя 1 с сигмой (n).
В 1997 году математик Карл Померанс сделал интригующее заявление о том, что одиночные числа обладают положительной плотностью — мерой того, насколько часто определенные элементы или объекты встречаются в данном наборе или популяции.
Заявление бросило вызов гипотезе Андерсона и Хикерсона 1977 года, однако доказательство так и не было опубликовано, и проблема остается нерешённой. Классификация чисел на дружественные и одиночные представляет собой сложную задачу в теории чисел.
Рассмотрим число 10, одно из самых маленьких чисел неизвестной классификации, предположительно одиночное. Если число не одиноко, то его наименьший друг, по оценкам, будет невероятно большим числом, порядка 1030.
В 2022 году Сурав Мандал пролил свет на потенциальную природу «друга» числа 10, предложив конкретную форму, которой этот «друг» должен следовать, если он существует. Более того, такие примеры, как число 24, классифицированное как дружественное и имеющее в качестве наименьшего друга число 91 963 648, иллюстрируют разнообразие в классификации чисел как дружественных или одиночных.
Математические задачи, многие из которых существуют уже столетия, подчеркивают не только бесконечность и сложность математической вселенной, но и непрекращающееся стремление человечества к знаниям и пониманию. Они напоминают нам о том, что математика – это не просто набор правил и формул, но живая, развивающаяся дисциплина, полная загадок и красоты.

На решение многих математических задач у математиков уходят десятилетия и даже столетия, в то время как другие задачи даже не поддаются решению. Любой, кто сможет решить некоторые из нерешенных задач, получит значительное финансовое вознаграждение, что поощрит математиков принять такой вызов.
1. Гипотеза Коллатца
Гипотеза Коллатца, которую иногда называют дилемма 3n+1 или HOTPO (Half Or Triple Plus One), считается одной из самых известных нерешённых головоломок в математике. Коллатц пытается ответить на, казалось бы, простой вопрос: может ли серия основных арифметических операций преобразовать любое положительное целое число в 1?Гипотеза Коллатца включает в себя генерацию последовательностей целых чисел, где каждое число получается из предыдущего по двум правилам. Начиная с любого положительного целого числа, если число четное, то его следует разделить на 2, а если нечетное — умножить на 3 и добавить 1, и в конечном итоге последовательность всегда достигнет числа 1.
Например, если мы начнем с числа 5, следующим числом будет 3x5+1, что равно 16. Поскольку 16 четное, мы разделим его на 2, чтобы получить следующее число в последовательности: 8. Это продолжается до тех пор, пока оно не достигнет 1. В итоге последовательность будет такой: 5, 16, 8, 4, 2, 1.
Главный вопрос гипотезы – всегда ли эта последовательность достигнет 1, независимо от начального положительного целого числа? Гипотеза Коллатца была выдвинута немецким математиком Лотаром Коллатцем в 1937 году, всего через 2 года после того, как он получил докторскую степень.
На протяжении многих лет математики пытались разгадать тайну гипотезы Коллатца, но она так и осталась загадкой. Многие математики предполагают, что эта проблема может быть даже вне досягаемости современной математики. Несмотря на многочисленные усилия, вложенные в исследование гипотезы, она остается нерешенной, и математическое сообщество продолжает бороться с ее тонкостями
2. Гипотеза Гольдбаха.
Гипотеза Гольдбаха — один из самых известных нерешенных вопросов теории чисел и математики. Гипотеза предполагает, что каждое четное натуральное число больше 2 можно представить в виде суммы двух простых чисел. Например: 16 = 3 + 13Гипотеза была впервые предложена Кристианом Гольдбахом в письме Леонарду Эйлеру от 7 июня 1742 года. В этом письме Гольдбах представил идею и предположил, что каждое целое число, большее 2, можно выразить как сумму трех простых чисел.
Эйлер в своем ответе счел первую часть гипотезы Гольдбаха весьма вероятной, заявив, что «всякое четное целое число является суммой двух простых чисел», хотя и не смог предоставить доказательства.
За прошедшие годы был достигнут значительный прогресс в понимании этой гипотезы. Например, Нильс Пиппинг проверил это утверждение до n = 100 000 в 1938 году, а позже, с появлением компьютеров, Т. Оливейра и Сильва провел распределенный компьютерный поиск, который подтвердил гипотезу для n, меньшего или равного 4×1018. (и перепроверено до 4×1017) к 2013 году.
Однако полное и строгое доказательство для всех четных целых чисел больше 2 остается неуловимым.
3. Гипотеза о простых числах-близнецах
Гипотеза о простых числах-близнецах — это одна из старейших и наиболее известных нерешённых проблем в теории чисел. Она утверждает, что существует бесконечно много пар простых чисел, разность между которыми равна двум. Например, числа 3 и 5 являются простыми числами-близнецами, потому что оба являются простыми, и их разность равна 2 (5 - 3 = 2).Другими словами, если p является простым числом, то существует вероятность, что p+2 тоже будет простым числом, и эти два простых числа будут образовывать пару простых чисел-близнецов. Примеры пар простых чисел-близнецов: (3, 5), (11, 13), (17, 19), (29, 31) и так далее.
Доказательство гипотезы о простых числах-близнецах долгое время было открытым вопросом в теории чисел. Первоначально это было предложено Альфонсом де Полиньяком в 1849 году, предполагавшим, что для каждого натурального числа k существует бесконечно много простых чисел p, таких что p+2k также является простым. Случай k=1 — это конкретная гипотеза о простых числах-близнецах, на которой мы сосредоточены.
В 2013 году работа математика Итана Чжана ознаменовала значительный шаг на пути к доказательству существования бесконечного числа простых чисел-близнецов. Исследования Чжана показали, что существует конечная верхняя граница – 70 миллионов – для которой промежутки между парами простых чисел сохраняются бесконечно часто.
В 2014 году граница (разница между двумя простыми числами) сократилась до 246, что указывает на значительный прогресс в понимании простых чисел-близнецов.
4. Гипотеза Римана
Гипотеза Римана касается поведения дзета-функции Римана — математической функции, используемой для изучения распределения простых чисел в комплексной плоскости. Риман утверждает, что все нетривиальные нули дзета-функции Римана лежат на определенной критической линии в комплексной плоскости. Мы можем думать об этой критической линии как о натянутом канате, и вопрос в том, изящно ли балансируют все эти нули на этой линии.
История гипотезы Римана начинается в XIX веке с немецкого математика Бернхарда Римана. В 1859 году Риман опубликовал основополагающую статью под названием «О количестве простых чисел, меньших заданной величины» (On the Number of Prime Numbers less than a Given Quantity). На страницах документа математик представил дзета-функцию ζ(s), комплексную функцию комплексной переменной 's'. Открытие Римана было революционным, поскольку оно потенциально могло раскрыть тайны простых чисел.
Гипотеза Римана имеет еще значительный вес в математическом мире благодаря ее включению в престижную «Задачу тысячелетия». В 2000 году Институт математики Клея признал гипотезу одной из семи выдающихся математических задач и предложил приз в 1 миллион долларов тому, кто сможет предоставить правильное доказательство одной из семи задач.
Сущность значения гипотезы Римана заключается в ее связи с теоремой о простых числах. В частности, если гипотеза Римана будет доказана или опровергнута, то многие важные теоремы о простых числах, опирающиеся в доказательстве на гипотезу Римана, станут либо истинными, либо ложными.
5. Существование нечетных совершенных чисел
Совершенное число – это положительное целое число, которое равно сумме всех своих положительных делителей, исключая само себя. Например, 6 – совершенное число, потому что его делители 1, 2, и 3 в сумме дают 6.Или другой хорошо известный пример совершенного числа — 28, делители которого равны 1, 2, 4, 7 и 14, и в сумме (1 + 2 + 4 + 7 + 14) дают 28.
Однако остается неясным, существуют ли какие-либо нечетные совершенные числа.
Правило Евклида для нахождения совершенных чисел заключается в том, что если 2n – 1 является простым числом (такое число называется простым числом Мерсенна), то 2n-1 (2n – 1) будет совершенным числом. Все известные совершенные числа были найдены именно таким образом и все они четные.
Жак Лефевр в 1496 году предположил, что все совершенные числа могут быть найдены по правилу Евклида, что подразумевает, что нечетных совершенных чисел не существует. Леонард Эйлер в свою очередь заметил, что вопрос о существовании нечетных совершенных чисел является чрезвычайно трудным и до сих пор не решенным.
Карл Померанс в более позднее время представил эвристический аргумент, утверждающий, что вероятность существования нечетных совершенных чисел очень мала. Это не доказывает их отсутствие, но усиливает сомнения в их существовании. Таким образом, несмотря на многовековые исследования, вопрос о существовании нечетных совершенных чисел остается открытым и является одной из загадок в теории чисел.
6. Являются ли числа трансцендентными?
Рассматриваемая проблема вращается вокруг трансцендентной природы некоторых математических констант, в частности константы Эйлера-Машерони (γ) и суммы π (pi) и e (числа Эйлера).
Трансцендентное число — это число, которое не является корнем какого-либо ненулевого полиномиального уравнения с целыми коэффициентами. Проще говоря, трансцендентные числа не могут быть выражены как решение полиномиального уравнения, в котором коэффициенты являются целыми числами.
Полиномиальное уравнение — это математическое уравнение, в котором полином равен нулю. Полином – математическое выражение, состоящее из переменных и коэффициентов, которые соединяются операциями сложения, вычитания, умножения и ненулевыми целочисленными степенями переменных. Например, x2+3x+2 является полиномом
Константа Эйлера-Машерони, обозначаемая как γ, является фундаментальной математической константой, которая возникает в различных областях математики, включая теорию чисел и исчисление.
Трансцендентный статус был предметом предположений в течение многих лет. Хотя существуют существенные доказательства, указывающие на трансцендентную природу γ, строгое доказательство остается нераскрытым.
Аналогично, сумма π и e является еще одним примером. И π, и e — трансцендентные числа, и ожидается, что их сумма также будет трансцендентной. Однако эта гипотеза еще не была окончательно доказана, что добавляет элемент загадочности в математический мир.
Статус этих констант как трансцендентных или нет, выходит за рамки математического любопытства и имеет значение в различных математических дисциплинах.
7. Проблема одиночного числа
Проблема одиночного числа углубляется в область одиночных чисел, которые представляют собой целые числа, не имеющие «друзей» в математическом смысле (например, они не имеют общего отношения ни с какими другими числами). Дружественные числа — это те, которые имеют одинаковый показатель изобилия (отношение суммы делителей числа к самому числу).К одиночным числам относятся простые числа, степени простых чисел и те числа, у которых наибольший общий делитель числа и сумма его делителей (обозначаемая как сигма (n)) равны 1. Например, цифра 5 — это одиночное число. Делителями 5 являются 1 и 5, а их сумма равна 6. Наибольший общий делитель 5 и 6 равен 1.
Хотя одиночество некоторых чисел можно доказать, исследуя их свойства, есть другие, для которых доказательство одиночества является сложной задачей. Например, считается, что такие числа, как 10, 15, 20 и многие другие, являются одиночными, но убедительного доказательства не существует.
Концепция одиночных чисел уже много лет интригует математиков. Хотя простые числа являются хорошо известными одиночными числами, другие целые числа также демонстрируют одиночество, даже если они не имеют общего наибольшего общего делителя 1 с сигмой (n).
В 1997 году математик Карл Померанс сделал интригующее заявление о том, что одиночные числа обладают положительной плотностью — мерой того, насколько часто определенные элементы или объекты встречаются в данном наборе или популяции.
Заявление бросило вызов гипотезе Андерсона и Хикерсона 1977 года, однако доказательство так и не было опубликовано, и проблема остается нерешённой. Классификация чисел на дружественные и одиночные представляет собой сложную задачу в теории чисел.
Рассмотрим число 10, одно из самых маленьких чисел неизвестной классификации, предположительно одиночное. Если число не одиноко, то его наименьший друг, по оценкам, будет невероятно большим числом, порядка 1030.
В 2022 году Сурав Мандал пролил свет на потенциальную природу «друга» числа 10, предложив конкретную форму, которой этот «друг» должен следовать, если он существует. Более того, такие примеры, как число 24, классифицированное как дружественное и имеющее в качестве наименьшего друга число 91 963 648, иллюстрируют разнообразие в классификации чисел как дружественных или одиночных.
Заключение
Это первая часть нашего увлекательного путешествия в мир математики. В этой статье мы углубились в увлекательный и сложный мир математики, исследуя ряд знаменитых, но до сих пор нерешенных задач, которые продолжают вызывать интерес и стимулировать умы математиков по всему миру. От гипотезы Коллатца до проблемы одиночных чисел, каждая из этих задач представляет собой не только головоломку, но и окно в глубины математического познания.Математические задачи, многие из которых существуют уже столетия, подчеркивают не только бесконечность и сложность математической вселенной, но и непрекращающееся стремление человечества к знаниям и пониманию. Они напоминают нам о том, что математика – это не просто набор правил и формул, но живая, развивающаяся дисциплина, полная загадок и красоты.
Для просмотра ссылки необходимо нажать
Вход или Регистрация